BINOMVERT-Funktion
Gibt die Binomialverteilungswahrscheinlichkeit der einzelnen Terme zurück. Verwenden Sie BINOMVERT bei Problemen mit einer festen Anzahl von Tests oder Versuchen, wenn die Ergebnisse eines Versuchs nur Erfolg oder Misserfolg sind, wenn die Versuche unabhängig sind und wenn die Erfolgswahrscheinlichkeit während des gesamten Experiments konstant ist. Beispielsweise kann BINOMVERT die Wahrscheinlichkeit berechnen, dass zwei der nächsten drei geborenen Babys männlich sind.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die möglicherweise eine verbesserte Genauigkeit bieten und deren Namen ihre Verwendung besser widerspiegeln. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie ab sofort die neuen Funktionen verwenden, da diese Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar ist.
Weitere Informationen zur neuen Funktion finden Sie unter BINOM.DIST-Funktion .
Syntax
BINOMVERT(Anzahl_s,Versuche,Wahrscheinlichkeit_s,kumulativ)
Die Syntax der BINOMVERT-Funktion hat die folgenden Argumente:
Number_s Erforderlich. Die Anzahl der Erfolge in Prüfungen.
Versuche erforderlich. Die Anzahl der unabhängigen Studien.
Wahrscheinlichkeit_s Erforderlich. Die Erfolgswahrscheinlichkeit bei jedem Versuch.
Kumulativ erforderlich. Ein logischer Wert, der die Form der Funktion bestimmt. Wenn kumulativ TRUE ist, gibt BINOMVERT die kumulative Verteilungsfunktion zurück, die die Wahrscheinlichkeit darstellt, dass es höchstens number_s Erfolge gibt; wenn FALSE, gibt es die Wahrscheinlichkeits-Massenfunktion zurück, die die Wahrscheinlichkeit ist, dass es number_s Erfolge gibt.
Bemerkungen
Number_s und Trials werden auf ganze Zahlen gekürzt.
Wenn Anzahl_s, Versuche oder Wahrscheinlichkeit_s nicht numerisch ist, gibt BINOMVERT den #WERT! Fehlerwert.
Wenn Anzahl_s < 0 oder Anzahl_s > Versuche, gibt BINOMVERT die #NUM! Fehlerwert.
Wenn Wahrscheinlichkeit_s < 0 oder Wahrscheinlichkeit_s > 1, gibt BINOMVERT die #NUM! Fehlerwert.
Wenn x = Anzahl_s, n = Versuche und p = Wahrscheinlichkeit_s, dann ist die binomiale Wahrscheinlichkeitsmassenfunktion:
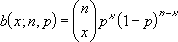
wo:

ist COMBIN(n,x).
Wenn x = Anzahl_s, n = Versuche und p = Wahrscheinlichkeit_s, dann ist die kumulative Binomialverteilung:
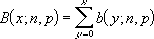
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Damit Formeln Ergebnisse anzeigen, wählen Sie sie aus, drücken Sie F2 und dann die EINGABETASTE. Bei Bedarf können Sie die Spaltenbreite anpassen, um alle Daten anzuzeigen.
Daten | Beschreibung | |
6 | Anzahl der Erfolge in Versuchen | |
10 | Anzahl unabhängiger Versuche | |
0,5 | Erfolgswahrscheinlichkeit bei jedem Versuch | |
Formel | Beschreibung | Ergebnis |
=BINOMVERT(A2,A3,A4,FALSCH) | Wahrscheinlichkeit, dass genau 6 von 10 Versuchen erfolgreich sind. | 0,2050781 |
No comments:
Post a Comment