RGP-Funktion
Dieser Artikel beschreibt die Formelsyntax und die Verwendung der RGP- Funktion in Microsoft Excel. Links zu weiteren Informationen zum Erstellen von Diagrammen und Durchführen einer Regressionsanalyse finden Sie im Abschnitt „ Siehe auch ".
Beschreibung
Die RGP- Funktion berechnet die Statistik für eine Linie, indem sie die Methode der "kleinsten Quadrate" verwendet, um eine gerade Linie zu berechnen, die am besten zu Ihren Daten passt, und gibt dann ein Array zurück, das die Linie beschreibt. Sie können RGP auch mit anderen Funktionen kombinieren, um die Statistiken für andere Typen von Modellen zu berechnen, die in den unbekannten Parametern linear sind, einschließlich polynomischer, logarithmischer, exponentieller und Potenzreihen. Da diese Funktion ein Array von Werten zurückgibt, muss sie als Matrixformel eingegeben werden. Anweisungen folgen den Beispielen in diesem Artikel.
Die Gleichung für die Linie lautet:
y = mx + b
-oder-
y = m1x1 + m2x2 + ... + b
wenn es mehrere Bereiche von x-Werten gibt, wobei die abhängigen y-Werte eine Funktion der unabhängigen x-Werte sind. Die m-Werte sind Koeffizienten, die jedem x-Wert entsprechen, und b ist ein konstanter Wert. Beachten Sie, dass y, x und m Vektoren sein können. Das Array, das die RGP -Funktion zurückgibt, ist {mn,mn-1,...,m1,b}. RGP kann auch zusätzliche Regressionsstatistiken zurückgeben.
Syntax
RGP(bekannte_y's, [bekannte_x's], [const], [stats])
Die Syntax der RGP-Funktion hat die folgenden Argumente:
Syntax
Bekannte_y ist Erforderlich. Der Satz von y-Werten, die Sie bereits in der Beziehung y = mx + b kennen.
Wenn sich der Bereich von known_y in einer einzelnen Spalte befindet, wird jede Spalte von known_x als separate Variable interpretiert.
Wenn der Bereich der bekannten_y in einer einzelnen Zeile enthalten ist, wird jede Zeile der bekannten_x als separate Variable interpretiert.
Bekannte_x Optional. Eine Reihe von x-Werten, die Sie möglicherweise bereits in der Beziehung y = mx + b kennen.
Der Bereich bekannter_x kann einen oder mehrere Sätze von Variablen enthalten. Wenn nur eine Variable verwendet wird, können die bekannten_y und die bekannten_x Bereiche beliebiger Form sein, solange sie die gleichen Dimensionen haben. Wenn mehr als eine Variable verwendet wird, muss known_y ein Vektor sein (dh ein Bereich mit einer Höhe von einer Zeile oder einer Breite von einer Spalte).
Wenn „known_x" weggelassen wird, wird davon ausgegangen, dass es sich um das Array {1,2,3,...} handelt, das dieselbe Größe wie „known_y" hat .
const Optional. Ein logischer Wert, der angibt, ob die Konstante b auf 0 gesetzt werden soll.
Wenn const TRUE ist oder weggelassen wird, wird b normal berechnet.
Wenn const FALSE ist, wird b gleich 0 gesetzt und die m-Werte werden so angepasst, dass sie zu y = mx passen.
Statistiken Optional. Ein logischer Wert, der angibt, ob zusätzliche Regressionsstatistiken zurückgegeben werden sollen.
Wenn Statistik TRUE ist, gibt RGP die zusätzliche Regressionsstatistik zurück; als Ergebnis ist das zurückgegebene Array {mn,mn-1,...,m1,b;sen,sen-1,...,se1,seb;r 2 ,sey;F,df;ssreg,ssresid} .
Wenn stats FALSE ist oder weggelassen wird, gibt RGP nur die m-Koeffizienten und die Konstante b zurück.
Die zusätzlichen Regressionsstatistiken lauten wie folgt.
Statistik | Beschreibung |
|---|---|
se1,se2,...,sen | Die Standardfehlerwerte für die Koeffizienten m1,m2,...,mn. |
seb | Der Standardfehlerwert für die Konstante b (seb = #N/A wenn const FALSE ist). |
r 2 | Das Bestimmtheitsmaß. Vergleicht geschätzte und tatsächliche y-Werte und reicht von 0 bis 1. Wenn es 1 ist, gibt es eine perfekte Korrelation in der Stichprobe – es gibt keinen Unterschied zwischen dem geschätzten y-Wert und dem tatsächlichen y-Wert. Wenn das Bestimmtheitsmaß dagegen 0 ist, ist die Regressionsgleichung nicht hilfreich, um einen y-Wert vorherzusagen. Informationen zur Berechnung von r 2 finden Sie unter „Hinweise" weiter unten in diesem Thema. |
Sey | Der Standardfehler für die y-Schätzung. |
F | Die F-Statistik oder der beobachtete F-Wert. Verwenden Sie die F-Statistik, um zu bestimmen, ob die beobachtete Beziehung zwischen den abhängigen und unabhängigen Variablen zufällig auftritt. |
df | Die Freiheitsgrade. Verwenden Sie die Freiheitsgrade, um F-kritische Werte in einer statistischen Tabelle zu finden. Vergleichen Sie die Werte, die Sie in der Tabelle finden, mit der F-Statistik, die von RGP zurückgegeben wird, um ein Konfidenzniveau für das Modell zu bestimmen. Informationen zur Berechnung von df finden Sie unter „Hinweise" weiter unten in diesem Thema. Beispiel 4 zeigt die Verwendung von F und df. |
ssreg | Die Summe der Quadrate der Regression. |
ssresid | Die Residualsumme der Quadrate. Informationen zur Berechnung von ssreg und ssresid finden Sie unter „Hinweise" weiter unten in diesem Thema. |
Die folgende Abbildung zeigt die Reihenfolge, in der die zusätzlichen Regressionsstatistiken zurückgegeben werden.

Bemerkungen
Mit der Steigung und dem y-Achsenabschnitt kann man jede beliebige Gerade beschreiben:
Steigung (m):
Um die Steigung einer Geraden zu finden, die oft als m geschrieben wird, nehmen Sie zwei Punkte auf der Geraden, (x1,y1) und (x2,y2); die Steigung ist gleich (y2 - y1)/(x2 - x1).Y-Achsenabschnitt (b):
Der y-Achsenabschnitt einer Linie, oft als b geschrieben, ist der Wert von y an dem Punkt, an dem die Linie die y-Achse kreuzt.Die Geradengleichung lautet y = mx + b. Sobald Sie die Werte von m und b kennen, können Sie jeden Punkt auf der Linie berechnen, indem Sie den y- oder x-Wert in diese Gleichung einsetzen. Sie können auch die TREND- Funktion verwenden.
Wenn Sie nur eine unabhängige x-Variable haben, können Sie die Werte für Steigung und y-Achsenabschnitt direkt erhalten, indem Sie die folgenden Formeln verwenden:
Neigung:
=INDEX(LINEST(bekannte_y,bekannte_x),1)Y-Achsenabschnitt:
=INDEX(LINEST(bekannte_y,bekannte_x),2)Die Genauigkeit der von der RGP- Funktion berechneten Linie hängt vom Grad der Streuung in Ihren Daten ab. Je linearer die Daten, desto genauer das RGP- Modell. RGP verwendet die Methode der kleinsten Quadrate, um die beste Anpassung für die Daten zu ermitteln. Wenn Sie nur eine unabhängige x-Variable haben, basieren die Berechnungen für m und b auf den folgenden Formeln:
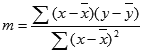
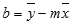
wobei x und y Stichprobenmittelwerte sind; das heißt, x = AVERAGE(bekannte x's) und y = AVERAGE( known_y's ) .
Die Linien- und Kurvenanpassungsfunktionen RGP und LOGEST können die beste gerade Linie oder Exponentialkurve berechnen, die zu Ihren Daten passt. Sie müssen sich jedoch entscheiden, welches der beiden Ergebnisse am besten zu Ihren Daten passt. Sie können TREND( bekannte_y's,bekannte_x's ) für eine gerade Linie oder GROWTH( bekannte_y's , bekannte_x's ) für eine Exponentialkurve berechnen. Diese Funktionen geben ohne das Argument von new_x ein Array von y-Werten zurück, die entlang dieser Linie oder Kurve an Ihren tatsächlichen Datenpunkten vorhergesagt wurden. Anschließend können Sie die prognostizierten Werte mit den tatsächlichen Werten vergleichen. Sie können beide für einen visuellen Vergleich grafisch darstellen.
Bei der Regressionsanalyse berechnet Excel für jeden Punkt die quadrierte Differenz zwischen dem für diesen Punkt geschätzten y-Wert und seinem tatsächlichen y-Wert. Die Summe dieser quadrierten Differenzen wird als Residualsumme der Quadrate ssresid bezeichnet. Excel berechnet dann die Gesamtsumme der Quadrate, stotal. Wenn das Argument const = TRUE ist oder weggelassen wird, ist die Gesamtsumme der Quadrate die Summe der quadrierten Differenzen zwischen den tatsächlichen y-Werten und dem Durchschnitt der y-Werte. Wenn das Argument const = FALSE ist, ist die Gesamtsumme der Quadrate die Summe der Quadrate der tatsächlichen y-Werte (ohne Subtraktion des durchschnittlichen y-Werts von jedem einzelnen y-Wert). Dann kann die Regressionsquadratsumme ssreg ermittelt werden aus: ssreg = stotal - ssresid. Je kleiner die Residualquadratsumme im Vergleich zur Gesamtquadratsumme ist, desto größer ist der Wert des Bestimmtheitsmaßes r 2 , das ein Maß dafür ist, wie gut die aus der Regressionsanalyse resultierende Gleichung den Zusammenhang zwischen den Variablen erklärt . Der Wert von r 2 ist gleich ssreg/stotal.
In einigen Fällen haben eine oder mehrere der X-Spalten (unter der Annahme, dass sich Ys und Xs in Spalten befinden) möglicherweise keinen zusätzlichen Vorhersagewert in Anwesenheit der anderen X-Spalten. Mit anderen Worten, das Eliminieren einer oder mehrerer X-Spalten kann zu vorhergesagten Y-Werten führen, die gleich genau sind. In diesem Fall sollten diese redundanten X-Spalten aus dem Regressionsmodell weggelassen werden. Dieses Phänomen wird „Kollinearität" genannt, da jede redundante X-Spalte als Summe von Vielfachen der nichtredundanten X-Spalten ausgedrückt werden kann. Die RGP- Funktion überprüft Kollinearität und entfernt alle redundanten X-Spalten aus dem Regressionsmodell, wenn sie sie identifiziert. Entfernte X-Spalten können in der RGP- Ausgabe als 0-Koeffizienten zusätzlich zu 0-Se-Werten erkannt werden. Wenn eine oder mehrere Spalten als redundant entfernt werden, ist df davon betroffen, da df von der Anzahl der tatsächlich für Vorhersagezwecke verwendeten X-Spalten abhängt. Einzelheiten zur Berechnung von df siehe Beispiel 4 . Wenn df geändert wird, weil redundante X-Spalten entfernt werden, sind auch die Werte von sey und F betroffen. Kollinearität sollte in der Praxis relativ selten sein. Ein Fall, in dem es wahrscheinlicher auftritt, ist jedoch, wenn einige X-Spalten nur 0- und 1-Werte als Indikatoren dafür enthalten, ob ein Proband in einem Experiment Mitglied einer bestimmten Gruppe ist oder nicht. Wenn const = TRUE oder weggelassen wird, fügt die RGP- Funktion effektiv eine zusätzliche X-Spalte mit allen 1-Werten ein, um den Schnittpunkt zu modellieren. Wenn Sie eine Spalte mit einer 1 für jedes Fach haben, wenn männlich, oder 0, wenn nicht, und Sie haben auch eine Spalte mit einer 1 für jedes Fach, wenn weiblich, oder 0, wenn nicht, ist diese letzte Spalte überflüssig, da Einträge darin sein können erhalten durch Subtrahieren des Eintrags in der Spalte „männlicher Indikator" von dem Eintrag in der zusätzlichen Spalte aller 1-Werte, die von der RGP- Funktion hinzugefügt wurden.
Der Wert von df wird wie folgt berechnet, wenn aufgrund von Kollinearität keine X-Spalten aus dem Modell entfernt werden: Wenn es k Spalten mit bekannten_x gibt und const = TRUE oder weggelassen wird, ist df = n – k – 1. Wenn const = FALSE, df = n - k. In beiden Fällen erhöht jede X-Spalte, die aufgrund von Kollinearität entfernt wurde, den Wert von df um 1.
Wenn Sie eine Array-Konstante (z. B. bekannt_x ) als Argument eingeben, verwenden Sie Kommas, um Werte zu trennen, die in derselben Zeile enthalten sind, und Semikolons, um Zeilen zu trennen. Trennzeichen können je nach Ihren regionalen Einstellungen unterschiedlich sein.
Beachten Sie, dass die von der Regressionsgleichung vorhergesagten y-Werte möglicherweise nicht gültig sind, wenn sie außerhalb des Bereichs der y-Werte liegen, die Sie zum Bestimmen der Gleichung verwendet haben.
Der zugrunde liegende Algorithmus, der in der RGP- Funktion verwendet wird, unterscheidet sich von dem zugrunde liegenden Algorithmus, der in den Funktionen SLOPE und INTERCEPT verwendet wird. Der Unterschied zwischen diesen Algorithmen kann zu unterschiedlichen Ergebnissen führen, wenn die Daten unbestimmt und kollinear sind. Wenn beispielsweise die Datenpunkte des Arguments von known_y 0 und die Datenpunkte des Arguments von known_x 1 sind:
RGP gibt den Wert 0 zurück. Der Algorithmus der RGP- Funktion ist darauf ausgelegt, vernünftige Ergebnisse für kollineare Daten zurückzugeben, und in diesem Fall kann mindestens eine Antwort gefunden werden.
SLOPE und INTERCEPT geben ein #DIV/0 zurück! Error. Der Algorithmus der Funktionen SLOPE und INTERCEPT sucht nur nach einer Antwort, und in diesem Fall kann es mehr als eine Antwort geben.
Neben der Verwendung von LOGEST zum Berechnen von Statistiken für andere Regressionstypen können Sie RGP verwenden, um eine Reihe anderer Regressionstypen zu berechnen, indem Sie Funktionen der x- und y-Variablen als x- und y-Reihen für RGP eingeben . Zum Beispiel die folgende Formel:
=LINEST(yvalues, xvalues^COLUMN($A:$C))
funktioniert, wenn Sie eine einzelne Spalte mit y-Werten und eine einzelne Spalte mit x-Werten haben, um die kubische Annäherung (Polynom der Ordnung 3) der Form zu berechnen:
y = m1*x + m2*x^2 + m3*x^3 + b
Sie können diese Formel anpassen, um andere Regressionstypen zu berechnen, aber in einigen Fällen erfordert dies die Anpassung der Ausgabewerte und anderer Statistiken.
Der F-Testwert, der von der RGP-Funktion zurückgegeben wird, unterscheidet sich von dem F-Testwert, der von der FTEST-Funktion zurückgegeben wird. RGP gibt die F-Statistik zurück, während FTEST die Wahrscheinlichkeit zurückgibt.
Beispiele
Beispiel 1 – Steigung und Y-Achsenabschnitt
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Damit Formeln Ergebnisse anzeigen, wählen Sie sie aus, drücken Sie F2 und dann die EINGABETASTE. Bei Bedarf können Sie die Spaltenbreite anpassen, um alle Daten anzuzeigen.
Bekannt y | X bekannt |
|---|---|
1 | 0 |
9 | 4 |
5 | 2 |
7 | 3 |
Ergebnis (Steigung) | Ergebnis (y-Achsenabschnitt) |
2 | 1 |
Formel (Array-Formel in den Zellen A7:B7) | |
=LINEST(A2:A5,B2:B5,,FALSCH) |
Beispiel 2 – Einfache lineare Regression
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Damit Formeln Ergebnisse anzeigen, wählen Sie sie aus, drücken Sie F2 und dann die EINGABETASTE. Bei Bedarf können Sie die Spaltenbreite anpassen, um alle Daten anzuzeigen.
Monat | Verkauf |
|---|---|
1 | 3.100 $ |
2 | 4.500 $ |
3 | 4.400 $ |
4 | 5.400 $ |
5 | 7.500 $ |
6 | 8.100 $ |
Formel | Ergebnis |
=SUMME(LINEST(B1:B6, A1:A6)*{9,1}) | 11.000 $ |
Berechnet die Schätzung der Verkäufe im neunten Monat basierend auf den Verkäufen in den Monaten 1 bis 6. |
Beispiel 3 – Mehrfache lineare Regression
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Damit Formeln Ergebnisse anzeigen, wählen Sie sie aus, drücken Sie F2 und dann die EINGABETASTE. Bei Bedarf können Sie die Spaltenbreite anpassen, um alle Daten anzuzeigen.
Grundfläche (x1) | Büros (x2) | Eingänge (x3) | Alter (x4) | Schätzwert (y) |
|---|---|---|---|---|
2310 | 2 | 2 | 20 | 142.000 $ |
2333 | 2 | 2 | 12 | 144.000 $ |
2356 | 3 | 1.5 | 33 | 151.000 $ |
2379 | 3 | 2 | 43 | 150.000 $ |
2402 | 2 | 3 | 53 | 139.000 $ |
2425 | 4 | 2 | 23 | 169.000 $ |
2448 | 2 | 1.5 | 99 | 126.000 $ |
2471 | 2 | 2 | 34 | 142.900 $ |
2494 | 3 | 3 | 23 | 163.000 $ |
2517 | 4 | 4 | 55 | 169.000 $ |
2540 | 2 | 3 | 22 | 149.000 $ |
-234.2371645 | ||||
13.26801148 | ||||
0,996747993 | ||||
459.7536742 | ||||
1732393319 | ||||
Formel (in A19 eingegebene dynamische Matrixformel) | ||||
=LINEST(E2:E12,A2:D12,WAHR,WAHR) |
Beispiel 4 – Verwendung der F- und r 2 -Statistik
Im vorherigen Beispiel beträgt das Bestimmtheitsmaß oder r 2 0,99675 (siehe Zelle A17 in der Ausgabe für RGP ), was auf eine starke Beziehung zwischen den unabhängigen Variablen und dem Verkaufspreis hindeuten würde. Ob diese Ergebnisse mit einem so hohen r2-Wert zufällig entstanden sind, können Sie anhand der F-Statistik feststellen.
Nehmen Sie für den Moment an, dass tatsächlich keine Beziehung zwischen den Variablen besteht, aber dass Sie eine seltene Stichprobe von 11 Bürogebäuden gezogen haben, die dazu führt, dass die statistische Analyse eine starke Beziehung zeigt. Der Begriff „Alpha" wird für die Wahrscheinlichkeit verwendet, fälschlicherweise auf einen Zusammenhang zu schließen.
Die F- und df-Werte in der Ausgabe der RGP- Funktion können verwendet werden, um die Wahrscheinlichkeit abzuschätzen, dass ein höherer F-Wert zufällig auftritt. F kann mit kritischen Werten in veröffentlichten F-Verteilungstabellen verglichen werden oder die FDIST -Funktion in Excel verwendet werden, um die Wahrscheinlichkeit zu berechnen, dass ein größerer F-Wert zufällig auftritt. Die geeignete F-Verteilung hat v1- und v2-Freiheitsgrade. Wenn n die Anzahl der Datenpunkte ist und const = TRUE oder weggelassen wird, dann ist v1 = n – df – 1 und v2 = df. (Wenn const = FALSE, dann v1 = n – df und v2 = df.) Die FDIST- Funktion – mit der Syntax FDIST (F,v1,v2) – gibt die Wahrscheinlichkeit zurück, dass ein höherer F-Wert zufällig auftritt. In diesem Beispiel ist df = 6 (Zelle B18) und F = 459,753674 (Zelle A18).
Unter der Annahme eines Alpha-Werts von 0,05, v1 = 11 – 6 – 1 = 4 und v2 = 6 beträgt das kritische Niveau von F 4,53. Da F = 459,753674 viel höher als 4,53 ist, ist es äußerst unwahrscheinlich, dass ein so hoher F-Wert zufällig aufgetreten ist. (Bei Alpha = 0,05 ist die Hypothese, dass es keinen Zusammenhang zwischen bekannten_y und bekannten_x gibt, abzulehnen, wenn F das kritische Niveau von 4,53 überschreitet.) Sie können die FDIST- Funktion in Excel verwenden, um die Wahrscheinlichkeit zu erhalten, dass ein so hoher F-Wert aufgetreten ist zufällig. Beispielsweise ist FDIST (459,753674, 4, 6) = 1,37E-7, eine extrem kleine Wahrscheinlichkeit. Sie können schlussfolgern, entweder indem Sie das kritische Niveau von F in einer Tabelle finden oder indem Sie die FDIST- Funktion verwenden, dass die Regressionsgleichung nützlich ist, um den geschätzten Wert von Bürogebäuden in diesem Bereich vorherzusagen. Denken Sie daran, dass es wichtig ist, die korrekten Werte von v1 und v2 zu verwenden, die im vorherigen Absatz berechnet wurden.
Beispiel 5 – Berechnung der t-Statistik
Ein weiterer Hypothesentest bestimmt, ob jeder Neigungskoeffizient beim Schätzen des geschätzten Werts eines Bürogebäudes in Beispiel 3 nützlich ist. Um beispielsweise den Alterskoeffizienten auf statistische Signifikanz zu testen, dividieren Sie -234,24 (Alterssteigungskoeffizient) durch 13,268 (der geschätzte Standardfehler der Alterskoeffizienten in Zelle A15). Das Folgende ist der t-beobachtete Wert:
t = m4 ÷ se4 = -234,24 ÷ 13,268 = -17,7
Wenn der Absolutwert von t ausreichend hoch ist, kann gefolgert werden, dass der Steigungskoeffizient nützlich ist, um den Schätzwert eines Bürogebäudes in Beispiel 3 zu schätzen. Die folgende Tabelle zeigt die Absolutwerte der 4 t-beobachteten Werte.
Wenn Sie eine Tabelle in einem Statistikhandbuch konsultieren, werden Sie feststellen, dass t-kritisch, zweiseitig, mit 6 Freiheitsgraden und Alpha = 0,05 2,447 ist. Dieser kritische Wert kann auch mithilfe der TINV- Funktion in Excel ermittelt werden. TINV (0,05,6) = 2,447. Da der Absolutwert von t (17,7) größer als 2,447 ist, ist das Alter eine wichtige Variable bei der Schätzung des Schätzwerts eines Bürogebäudes. Jede der anderen unabhängigen Variablen kann auf ähnliche Weise auf statistische Signifikanz getestet werden. Das Folgende sind die beobachteten t-Werte für jede der unabhängigen Variablen.
Variable | t-beobachteter Wert |
|---|---|
Bodenfläche | 5.1 |
Anzahl der Büros | 31.3 |
Anzahl der Eingänge | 4.8 |
Das Alter | 17.7 |
Diese Werte haben alle einen absoluten Wert größer als 2,447; Daher sind alle in der Regressionsgleichung verwendeten Variablen nützlich, um den geschätzten Wert von Bürogebäuden in diesem Bereich vorherzusagen.
No comments:
Post a Comment