ZTEST-Funktion
Dieser Artikel beschreibt die Formelsyntax und die Verwendung der ZTEST- Funktion in Microsoft Excel.
Gibt den einseitigen Wahrscheinlichkeitswert eines Z-Tests zurück. Für einen gegebenen hypothetischen Populationsmittelwert, μ0, gibt ZTEST die Wahrscheinlichkeit zurück, dass der Stichprobenmittelwert größer als der Durchschnitt der Beobachtungen im Datensatz (Array) wäre – d. h. der beobachtete Stichprobenmittelwert.
Um zu sehen, wie ZTEST in einer Formel verwendet werden kann, um einen zweiseitigen Wahrscheinlichkeitswert zu berechnen, siehe "Bemerkungen" unten.
Wichtig: Diese Funktion wurde durch eine oder mehrere neue Funktionen ersetzt, die möglicherweise eine verbesserte Genauigkeit bieten und deren Namen ihre Verwendung besser widerspiegeln. Obwohl diese Funktion aus Gründen der Abwärtskompatibilität weiterhin verfügbar ist, sollten Sie ab sofort die neuen Funktionen verwenden, da diese Funktion in zukünftigen Versionen von Excel möglicherweise nicht mehr verfügbar ist.
Weitere Informationen zur neuen Funktion finden Sie unterZ.TEST-Funktion .
Syntax
ZTEST(Array,x,[Sigma])
Die Syntax der ZTEST-Funktion hat die folgenden Argumente:
Array erforderlich. Das Array oder der Datenbereich, mit dem x getestet werden soll.
X Erforderlich. Der zu testende Wert.
Sigma Optional. Die (bekannte) Standardabweichung der Grundgesamtheit. Wenn weggelassen, wird die Standardabweichung der Stichprobe verwendet.
Bemerkungen
Wenn das Array leer ist, gibt ZTEST den Fehlerwert #NV zurück.
ZTEST wird wie folgt berechnet, wenn Sigma nicht weggelassen wird:
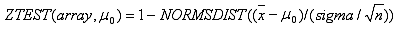
oder wenn Sigma weggelassen wird:
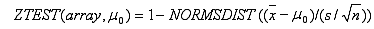
wobei x der Stichprobenmittelwert AVERAGE(array) ist; s ist die Stichproben-Standardabweichung STDEV(array); und n ist die Anzahl der Beobachtungen in der Stichprobe COUNT(array).
ZTEST stellt die Wahrscheinlichkeit dar, dass der Stichprobenmittelwert größer als der beobachtete Wert AVERAGE(array) wäre, wenn der zugrunde liegende Populationsmittelwert μ0 ist. Aufgrund der Symmetrie der Normalverteilung gibt ZTEST einen Wert größer als 0,5 zurück, wenn AVERAGE(array) < μ0 ist.
Die folgende Excel-Formel kann verwendet werden, um die zweiseitige Wahrscheinlichkeit zu berechnen, dass der Stichprobenmittelwert weiter von μ0 (in beide Richtungen) als AVERAGE(array) entfernt wäre, wenn der zugrunde liegende Mittelwert der Grundgesamtheit μ0 ist:
=2 * MIN(ZTEST(Array,μ0,Sigma), 1 - ZTEST(Array,μ0,Sigma)).
Beispiel
Kopieren Sie die Beispieldaten in der folgenden Tabelle, und fügen Sie sie in Zelle A1 eines neuen Excel-Arbeitsblatts ein. Damit Formeln Ergebnisse anzeigen, wählen Sie sie aus, drücken Sie F2 und dann die EINGABETASTE. Bei Bedarf können Sie die Spaltenbreite anpassen, um alle Daten anzuzeigen.
Daten | ||
3 | ||
6 | ||
7 | ||
8 | ||
6 | ||
5 | ||
4 | ||
2 | ||
1 | ||
9 | ||
Formel | Beschreibung (Ergebnis) | Ergebnis |
=ZTEST(A2:A11,4) | Einseitiger Wahrscheinlichkeitswert eines z-Tests für den obigen Datensatz bei dem hypothetischen Populationsmittelwert von 4 (0,090574) | 0,090574 |
=2 * MIN(ZTEST(A2:A11,4), 1 - ZTEST(A2:A11,4)) | Zweiseitiger Wahrscheinlichkeitswert eines z-Tests für den obigen Datensatz bei dem hypothetischen Populationsmittelwert von 4 (0,181148) | 0,181148 |
=ZTEST(A2:A11,6) | Einseitiger Wahrscheinlichkeitswert eines z-Tests für den obigen Datensatz bei dem hypothetischen Populationsmittelwert von 6 (0,863043) | 0,863043 |
=2 * MIN(ZTEST(A2:A11,6), 1 - ZTEST(A2:A11,6)) | Zweiseitiger Wahrscheinlichkeitswert eines z-Tests für den obigen Datensatz bei dem angenommenen Populationsmittelwert von 6 (0,273913) | 0,273913 |
No comments:
Post a Comment